종이 사용량은 절수를 완전히 이해해야만 가능합니다.
사실 절수는 나누기와 여분만 아시면 그리 어려울 것도 없습니다. 숫자가 나오면 본능적으로 알르레기를 일으키시는 분들도 이 기회에 눈에 힘을 주고 찬찬히 살펴보십시요.

우선 앞서 살펴본 바대로 재단여분와 인쇄여분을 충분히 고려하여 전지 1장에 나올 수 있는 절수를 계산합니다.

1.예를 들어 국배판(A4) 규격 297x210mm의 크기, 360쪽 분량의 책을 700부 인쇄한다면 본문 종이는 어떻게 계산하는가?

위의 조견표와 판형표를 참고하면 297☓210mm 크기의 판형은 국전지 1장에 8절 크기로 16쪽이 나올 수 있다면 거기에 전체 페이지수를 나눕니다. 360쪽의 책이라면 360쪽 나누기 16쪽 하면 22.5가 나옵니다. 22장반으로 한 권이 나오는 셈입니다. 거기에 부수를 곱하면 22.5매☓700부=15750매가 나오고 그것을 종이의 거래단위 연으로 나누면 31연 250매가 나옵니다. 이것이 정확한 국전 종이 8절 크기의 360쪽 책 700부의 종이 사용량이 됩니다.
그러나 여기에서 주의해야할 것은 반드시 인쇄할 때에는 핀을 맞춘다던가 색의 농도가 안정감을 찾을 때까지 여러 장의 사용할 수 없는 인쇄물 즉 파지가 나오게 되므로 종이는 정확한 양보다 여유있게 주문하여야합니다. 더욱이 인쇄의 난이도에 따라 종이여분이 더 필요하겠지만 통상 10% 내외로 잡으면 안전합니다. 부수가 많으면 비율은 낮아질 것이고 부수가 적으면 비율은 높아질 것입니다. 그래서 종이의 주문량은 국전지, 15750매☓10%=17325.5장이 되고 34연 326매를 주문하면 됩니다.
인쇄 외에 제본이나 코팅 등, 후가공의 여러 공정을 거쳐야하는 인쇄물일 경우에는 종이여분이 더욱 많이 필요합니다. 각 공정마다 파지가 필요하기 때문입니다.
인쇄뿐만 아니라 이후 공정에서 파지가 많이 발생할 경우 원하는 정확한 수량이 나오지 못하는 경우가 많습니다. 그래서 조금은 여유 있게 종이를 주문하시는 것이 좋습니다.
특히 책인 경우는 많은 페이지물 중 몇 쪽의 수가 모자라 한 권의 책으로 완성되지 못하는 안타까운 일도 있으니까요!

①책인 경우 1장에 원하는 판형의 펼침 면이 몇 절로 나오는지 혹은 몇 쪽이 나오는지 계산한다.(이때 재단여분과 인쇄여분을 고려하여 절수를 계산한다)
②전체 쪽수를 곱하여 1권에 전지 몇 장이 소요되는지 계산한다.
③거기에 필요한 부수를 곱하면 사용할 종이가 나온다.

종이 사용량은: 책 전체쪽수 나누기 전지 1장에 나오는 쪽수 곱하기 인쇄부수 곱하기 여분(10%) 나누기 500매(1연), 그리고 나머지
④꼭 필요한 종이 사용량(정량)에 다음공정에 필요한 파지의 여분을 더한다.

주의
이때 절수와 쪽수를 구별하지 않아 실수가 자주 발생합니다. 쪽수는 절수의 두 배입니다. 절수를 그대로 전체쪽수로 나누어 발생하는 실수가 많습니다. 쪽수와 절수와 판형을 정확하게 구별하여 계산하여야 합니다.
또 책은 가운데 제본이 되어야 하므로 최소한 4배수의 쪽수가 필요합니다. 그러나 접지를 기준으로 16쪽수 접지를 기준으로 만든 책이라면 16배수의 쪽수가 필요합니다. 이것이 대수를 맞춘다는 것입니다.(⇨인쇄파트에서 다시 설명하겠습니다.)
만일 16쪽수가 전지로 한 대인 책인데 16배수를 맞추기가 곤란하다면 적어도 그 반인 8배수는 맞추어야 인쇄가 가능합니다.

그리고 정확하게 배수로 떨어지지 않는 쪽수는 어떻게 인쇄하는지 많이 궁금해 합니다.
위의 예에서 1권이 22.5장이 소요되는데 0.5장은 반장만 필요하기 때문에 종이를 반으로 재단하여 700부 인쇄하기도 하고 때로는 0.5에 해당하는 필름을 두배 반복 출력하여 앉혀 전지로 만들어 700부을 돌리지 않고 350부만 인쇄하여 제본할 때 반으로 재단하여 700부를 만들어 사용하기도 합니다.
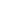
이 모든 것은 전지로 인쇄할 경우이고 반절로 인쇄할 때에는 16쪽의 반 8쪽이 한대가 됩니다.
그 경우에는 8배수의 혹은 그 반인 4배수까지 인쇄가 가능합니다.

전지로 인쇄할 경우 반절로 인쇄할 경우

또 위 그림에서 알 수있는 것은 인쇄무는 쪽의 방향이 바뀌었다는 것입니다.
인쇄할 절수에 따라 인쇄무는 쪽은 언제나 빠뀔 수있다는 것을 유념하십시요!
화살표시는 종이의 결을 나타냅니다. 이것도 종이를 재단하여 인쇄할 방향과 혼동해서는 안됩니다.

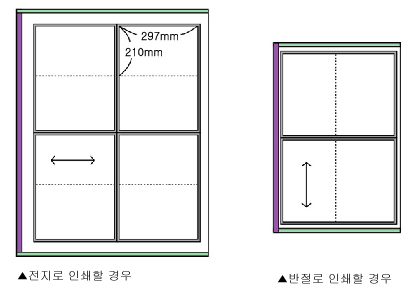
2. 카타로그라면 더욱 간단합니다. 224☓300mm크기의 16쪽 카타로그 3000부 인쇄하려면 어떻게 계산될까요? 여러분이 직접 해보는 것이 좋습니다. 나중에 답을 확인하세요!

① 16쪽이라면 4쪽의 낱장종이를 4장 붙인 셈입니다.
우선 두 쪽이 붙어 있는 상태 448☓300의 크기를 종이규격에서 찾아봅니다. 판형은 국 8절이지만 인쇄는 펼친 면으로 인쇄하기 때문에 국전지 4절로 470☓318 크기에 인쇄할 수 있는 계산이 나옵니다.
과연 이 절수가 맞는지 다시 확인해봅니다. 원래의 크기에서 사방 3mm씩 연장하여 454☓306mm으로 인쇄해야 하며 인쇄되지 않은 공간에 대한 고려를 한다면 (454☓306)☓2= 908☓613으로 짧은 면의 치수(인쇄기가 물고 들어가는 공간) 613mm가 전지 크기 636mm에 23mm 여유가 있기 때문에 충분히 인쇄할 수 있습니다. 넓은 면도 확인하면 939-908=31mm의 여유가 있기 때문에 가능한 절수가 됩니다.
이것은 반절인쇄기보다는 국전인쇄기에 한 대에 4절로 앉혀지게 인쇄하면 됩니다.

② 전지 한 장에 펼친 면 4절 쪽수로는 16쪽이 인쇄되기 때문에 1권 16쪽이 나오기 위해서는 전지 1장이 필요합니다. 한대에 한권이 나오게 되는 셈입니다.
③ 1권에 16쪽이 나오는 종이= 1장 ☓ 필요한 부수 3000부 = 3000매가 나옵니다.
④ 거기에 여분을 더하면 3000매 곱하기 1.1(10%)=3300매 이것을 거래단위로 나누면 6연300매로 이 카타로그 3000부를 인쇄하는데 필요한 양이 됩니다.

이때 인쇄의 도수나 별색 등 까다롭지 않은 인쇄이거나 후가공에서의 어려운 과정이 없다면 6연 300매의 종이를 제지업소에 주문하시면 됩니다.

종이여분10%는 종이량이 많으면 비율이 줄어들고 종이량이 적으면 늘어나기 마련이다.그리고 절수가 작게 인쇄되는 경우에는 적을 것이고 절수가 전지인 경우에는 많아질 수밖에 없다.

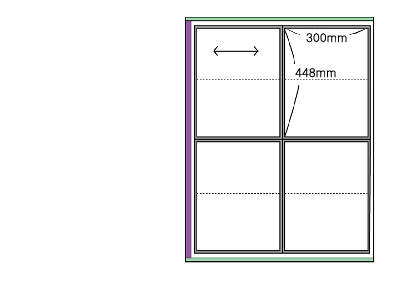
3. 280☓140mm 크기의 28쪽 브로쉬어 5000부를 인쇄하려면 종이가 어떻게 필요할까요?

그림을 그려볼까요? 이것은 세로보다 가로가 긴 독특한 인쇄물입니다.

①가로280 세로140mm의 크기라면 인쇄할 때는 펼친면 560☓140으로 인쇄하겠지요?
그래서 560☓140의 크기를 조견표에서 찾아보면 국6절 636☓157 의 크기가 나옵니다.
실제 크기에서 재단여분을 계산하면 566☓146의 크기가 될 것이고 장 6절이기 때문에 인쇄기에서의 여분을 고려한다면146☓6 =836(939-103)mm가 계산되고 103mm의 여분이 생기므로 인쇄여분이 가능하게 됩니다. 또 폭의 여분은 566(636-70)mm 로 폭도 70mm의 인쇄기가 무는(구와이)여분이 있으므로 이 브로쉬어는 국전지 장 6절로 인쇄가 가능하게 되겠지요!
② 전지 한 장에 앞뒤로 24쪽이 인쇄 됩니다. 28쪽이라면 1장(24쪽)과 4쪽이 남습니다. 대수가 맞는 1대는 5000부를 인쇄하려면 5000매의 종이가 필요합니다. 그리고 나머지 4쪽의 인쇄는 종이를 반절로 재단하고 필름을 3벌 반복 출력한 다음 각각 5000부를 인쇄해야하기 때문에 3벌 반복한 필름을 1667번 인쇄해야 5000부가 나옵니다. 그러나 이 3벌 반복한 종이의 크기는 국반절이기 때문에 1667/2= 834매로 이 4쪽을 인쇄하기위해선 834매의 종이가 필요합니다. 앞의 1대 5000매와 뒤의 반대 834를 더하면 5834매가 나옵니다. 이 브로쉬어 제작에 필요한 정확한 종이는 5834매이고 여분을 더하면☓1.1= 6418매가 계산되고 다시 이를 거래단위 500매=1연로 나누면 12연 418매의 종이를 인쇄소로 보내면 됩니다.

여기에서 표지가 본문과 다른 종이라면 더욱 간단하겠죠?
11연은 본문용 종이로 주문하고 1연 418매는 표지용 종이로 주문하면 아주 쉽죠!
역으로 확인해 볼까요? 나머지 4쪽으로 떨어진 부분이 걱정이 된다고요?
4쪽에 계산된 종이가 834매가 나왔습니다. 여분은 색각하지 않고 이 834매를 반절로 재단하면 1668장이 나옵니다. 다시 이 반절에는 같은 이미지를 3번 반복하였기 때문에 1668☓3 =5004로 5000부에 해당하는 이미지를 얻을 수 있게 됩니다.
1대는 전지에 인쇄하고 2대는 반절에 인쇄하게 됩니다.
③ 인쇄 후 과정의 코팅이나 금은 박 등이 없다면 이 브로쉬어의 종이 주문은 12연 418매가 됩니다.
④ 제본이 어느 쪽으로 되어있느냐에 따라서도 절수가 달라지고 인쇄하는 방법, 종이계산 방법 등이 달라질 수 있습니다.


다시 한번 강조
여분이 아주 중요합니다.
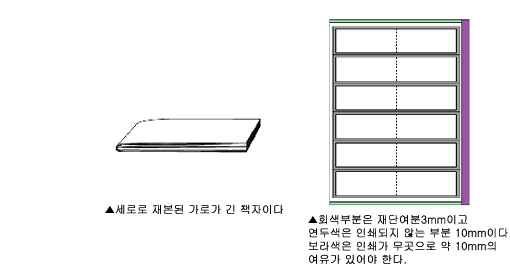
인쇄할 때에는 세 가지의 여분이 필요합니다.
첫 번째, 재단여분 3mm,
두 번째, 인쇄기에서 인쇄가 되지 않는 부분,(물리는 부분과 종이의 폭방향 바깥쪽)
세 번째, 종이 사용량에서의 여분, (공정상 필요한 파지)
이것만 정확하게 기억하고 있으면 절수를 계산하는 데는 큰 어려움은 없을 것입니다.

거의 다 왔습니다.
시골길을 안내하시던 할머니의 말씀이 아닙니다.
그 골치아픈 종이계산법이 지나갔으니 이제 거의 다 온셈입니다.



잠깐!! 반드시 확인하자 ‘종이결판별법’

종이를 선택할 때는 반드시 종이결을 알고 선택해야 합니다. 결의 반대방향으로 변형이 쉽게오기 때문입니다. 옷감에서도 식서방향이 있듯이 종이에도 결이 있습니다.
결은 육안으로 잘 나타나지 않지만 초지를 만들 때 펄프가 배열되는 형태가 종이결을 형성하게 됩니다. 이 펄프의 배열형태에 따라 종목, 횡목으로 종이를 구분합니다.
종이가 롤 형태로 생산되며 생산하여 쉬트지로 재단할 때 가로방향으로 재단하느냐? 세로방향으로 재단하느냐에 따라 종목(가로결), 횡목(세로결)로 나누어집니다.

잘못된 결로 책을 만들었을 때 책을 펼쳤을 때 제책한 자리가 뜯어지거나 책장이 잘 넘어가지 않으며 표지 같은 경우에는 바깥쪽으로 휘어 미관상 보기에 좋지 않습니다. 제본되는 쪽으로 결이 나 있는 것이 정상입니다.때로는 코팅없이 접지가 되어있는 두꺼운 인쇄물은 접지를 가한 쪽이 거칠게 터져 좋지 않은 결과를 초래하기도 합니다. 또 지금도 서점에 가면 잘못된 결로 인쇄된 책을 얼마든지 찾아볼 수 있습니다. 책을 오래 진열해 놓으면 표지가 제본이 되지 않은 바깥쪽으로 들떠 있는 책들이 대부분 잘못된 결로 사용한 책이라는 것을 보면 알 수 있습니다. 정확한 결로 사용하여야만 부드럽게 책장이 잘 넘어가고 기우는 현상이 없습니다.
따라서 종이를 선택할 때에는 종이의 규격뿐만 아니라 종이결도 반드시 확인해야 합니다. 손쉽게 알 수 있는 것은 신문을 손으로 찢어 보았을 때 깨끗이 찢기는 쪽이 있는가 하면 잘 찢기지 않는 쪽이 있음을 보면 알 수 있습니다. 잘 찢기는 쪽이 그 종이의 결입니다.

종이결을 판별하는 방법에는 찢어보기, 꺽어보기, 물에 적셔보기, 불빛에 반사하여 보기 등 여러가지 방법이 있으나 일반인들은 거의 판별하기 힘들고 가장 편리한 방법은 종이 구입시 포장지에 붙어있는 라벨을 확인해보는 것입니다. 즉 종목은 상표가 짧은 쪽에 붙어있고, 횡목은 긴방향 쪽에 붙어있습니다. 요즘엔 라벨자체에 종목, 횡목 구분을 하여 출시되고 있습니다.

또 하나의 방법은 규격표시를 보고 알 수 있습니다. 제지회사에서는 규격을 항상 가로*세로로 나타냅니다.
예를 들어, 788☓1091 규격은 가로 788mm, 세로 1091mm 를 의미하는데 가로규격보다 세로규격이 크면 세로결(종목) 종이이고, 가로규격이 세로규격보다 크면 가로결(횡목) 종이가 됩니다.
즉 46전지 종목(세로결)은 788☓1091로, 46전지 횡목(가로결)은 1091☓788로 표기됩니다.
국전지 종목(세로결)은 636☓939이로, 국전지 횡목(가로결)은 939☓636으로 표기됩니다.